可靠性試驗靈敏度分析的降階積分法

可靠性試驗靈敏度定義為失效概率對基本隨機變量分布參數(shù)的偏導數(shù)[3,4]。失效概率對第個變量的分布參數(shù)的可靠性試驗靈敏度可表示成式所示的形式。

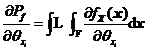
在5.1節(jié)中已經(jīng)給出了原坐標空間轉換成標準正態(tài)坐標空間的失效概率的計算公式，因此可靠性試驗靈敏度的求解方法可由復合函數(shù)求導法則寫成下面的形式。

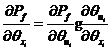
其中為第個變量所對應的標準正態(tài)化變量的分布參數(shù)。

對于相互獨立的正態(tài)變量的情況，有式成立[4]。

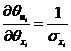
由式確定的失效概率Pf對基本隨機變量對應的標準正態(tài)化變量的分布參數(shù)的偏導數(shù)，利用復合函數(shù)求導法則求得如式所示。

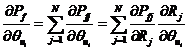
將式和式代入式中，可得失效概率對基本隨機變量分布參數(shù)的可靠性試驗靈敏度的計算公式如式所示。

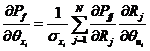
下面以相互獨立的二維和三維變量的情況為例來具體說明結構可靠性試驗靈敏度分析的降階積分法，對于其他維數(shù)的情況可以類似地推導。

對于二維變量的情況，可靠性試驗靈敏度可以表示成式對第個變量的分布參數(shù)求偏導數(shù)，有：

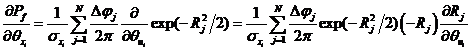
對于三維變量的情況，可靠性試驗靈敏度可以表示成式對第個變量的分布參數(shù)求偏導數(shù)，有

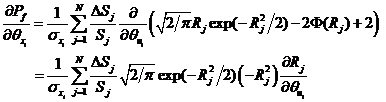
對于其他維數(shù)變量的情況，類似地可以推得失效概率對基本隨機變量分布參數(shù)的可靠性試驗靈敏度。